Diffusion Model

Denising Diffusion Probabilistic Models - https://ar5iv.org/html/2006.11239

Denoising Diffusion Probabilistic Models

Abstract(요약)

 diffusion probabilistic models을 이용한 고품질의 이미지 합성이 목표이며, 확산 확률 모델은 비평형 열역학에서 영감을 받은 잠재 변수 모델 클래스이며, 최상의 결과는 확산 확률 모델과 노이즈 제거 매칭 및 랑주뱅 동역학 사이의 새로운 연결을 바탕으로 설계된wighted variational bound를 학습하여 얻어졌다. 이 모델은 점진적 손실 압축 체계를 허용하고, autoregressive decoding의 일반화로 해석될 수 있다.

 

Introduction(주제)

 VAE, GAN 등의 발전과 함께, 에너지 기반 모델링과 스코어 매칭에도 큰 진전이 있었고, 이는 GAN 수준에 필적하는 이미지를 생성해냈는데, 이 논문의 Diffusion probabilistic model의 발전을 다루는게, 확산모델은 유한한 시간 후 데이터를 매칭 하는 샘플을 생성하도록 하는 variational inference를 사용해 학습되는 매개변수화된 마르코프 체인이다. 이 체인은 샘플링의 반대 방향으로 데이터를 점진적 노이즈화 하는 diffusion process를 역으로 수행하도록 학습되며, diffusion이 소량의 가우시안 노이즈를 사용하기에, 샘플링 체인을 조건부 가우시안 설정 하는 것으로 충분하고, 이를 통해 단순한 신경망으로 매개변수화 할 수 있다.

 확산 모델이 정의하기 쉽고 효율이 좋지만, 현재까지 고품질 샘플을 생성할 수 있음을 보여주지는 않는데, 이 연구는 확산 모델이 실제로 고품질 샘플을 생성할 수 있으며, 특정 파라미터가 훈련 중 여러 노이즈 수준에서 스코어 매칭과 샘플링 중의 annealed langevin dynamics와 동등함을 보여준다. 샘플 품질에 불구하고, 우리 다른 likelihood 기반 모델과 비교해서 경쟁력 있는 로그 가능도를 가지지 않는다만, 에너지 기반 모델과 스코어 매칭에 대해 큰 추정값보다 더 나은 로그가능도를 가진다. DDPM의 lossless codelength가 대부분 인지할 수 없는 이미지 세부 정보를 설명하는 데 사용되었다. Diffusion의 샘플링이 autoregressive model과 디코딩과 유사한 점진적 디코딩이라는 것을 보인다.

 

→기존 확산모델의 한계점인 고품질 이미지에 대한 생성 불가 문제를 풀고자 했다.

 

Background(배경)

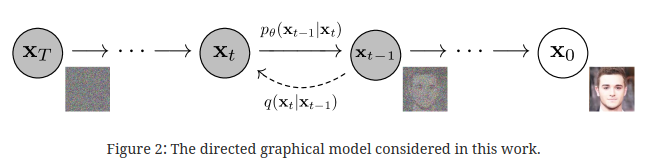
 DDPM의 핵심은 순차적으로, 그리고 픽셀간 독립적으로, 가우시안 기반의 noise를 추가했다가 제거하는 방식을 통해 재건하는 방식이라는 것이다. 두 과정을 거치며 학습을 진행하며 각각 forward process(diffusion process)(noise를 더하는 과정), reverse process(noise를 제거하는 과정) 으로 나뉜다. 즉 우리가 학습할 것은 noise를 지우는 방법으로, 그 평균과 분산 값에 대해 배울 것이다.

reverse proces

앞선 정보를 받아 (특정 시점 T에서 noise를 제거한 이미지) 를 해당 층의 denoise 작업을 통해 noise를 제거한다.

diffusion process

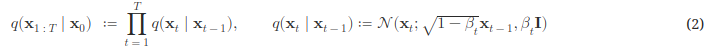
diffusion process는 noise를 더하는 과정이다. 이 때, 베타 값을 추가하여, 각 시점에 다른 베타값을 이용하여, 노이즈를 추가하는데, 어차피 정규분포에서 샘플링한 것들이라 이런 과정이 필요하지 않지 않나라는 생각이 들었고, 그에 대한 나의 해답은 다음과 같다. Forward pass에서의 noise 조절 : (1 - 베타)는 이전 값을 (pixel) 얼마나 반영할지에 대한 것이고, 베터는 그 중에서 얼마나 큰 분산값(불확실한 정도)를 바탕으로 노이즈를 추가할 것인가를 조절할 수 있게 해준다. 단순히 $x_{t-1}, I$ 를 사용할 때 보다 가질 수 있는 장점은 1. 학습 안정성 : 각 시점(층) 에서의 노이즈의 조절을 통해 학습에 관여할 수 있다.고 하지만, 그냥 생각해보면, 단순히 정규분포에서의 노이즈를 추가하고 제거하는 과정은 딱히 학습이 필요 없을 것 같다는 생각이 들어서, 그래서 베타를 넣지 않았나 생각한다.

 

ELBO term

학습을 할 때는 VAE와 마찬가지로 negative log likelihood를 최소화 하는 방식으로 학습을 한다. 이 수식이 이해가 가지 않는다면, 그건 당연한 것이다. VAE의 elbo term을 보고 유도 과정을 본다면 보다 쉽게 이해할 수 있을 것이다.

앞서 베타를 이용한 샘플링을 한다고 했는데, 이것을 diffusion process에 적용한다고 하면 문제가 되는 것이 auto regressive 로, 이전 state의 정보를 받아와야 된다는 문제가 생기는데, reverse process에서는 어쩔 수 없지만, diffusion process에서는 단순히 특정 시점의 베타 값들의 곱을 이용해 ahat 을 정의하고 이를 사용하는 방식을 사용할 수 있다.

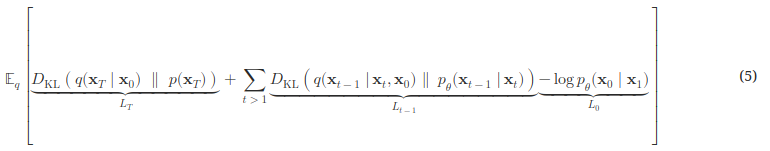
앞 서본 elbow term에서 t = 1을 빼내고, t -> t-1로 바꾸는 과정을 통해 보다 효율적인 loss function을 만들어 낼 수 있는데,

$L_T$ 는 p, q 즉 각 시점에서의 noise를 더하고 빼는 방식(평균, 분산)을 같게 학습하도록 하는 것이다.

$L_{t-1}$ 은 reverse process 와 diffusion process가 동일한 과정을 거칠 수 있게 학습하도록 하는 것이고,

$L_0$ 는 reconstruction term으로 원본으로 나올 가능성(우도)를 최대화 하게 하는 것이다.

 

이러한 과정을 통해 더이상 몬테카를로 법칙의 불확실성에 기대지 않는 loss term을 만들 수 있다.

Diffusion models and denoising autoencoders

DM이 마치 제한된 잠재변수모델처럼 보일 수 있지만, 구현상의 다양한 자유를 가능하게 하는데,  분산 베타나,